
Viaceré mosty sa blížia k hranici svojej životnosti
Hodnotenie spoľahlivosti a zostatkovej životnosti predpätých konštrukcií a mostov sa hlavne vo svetle niektorých nedávnych mimoriadnych udalostí stáva čoraz dôležitejším. Problematické predpäté mostné konštrukcie prvej generácie sú v prevádzke už viac ako šesťdesiat rokov, a tak je znalosť aktuálneho stavu ich predpätia základným vstupom pri každom statickom prepočte.
 |
Poznáte výhody Klubu ASB? Stačí bezplatná registrácia a získate sektorové analýzy slovenského stavebníctva s rebríčkami firiem ⟶ |
Táto skutočnosť vedie k potrebe overiť rôzne metódy, ktoré umožnia určiť aktuálnu hodnotu predpínacej sily. Príspevok nadväzuje na prácu tímu, ktorý sa na KSKM SvF UNIZA v Žiline už dlhodobo venuje výskumu spoľahlivosti predpätých konštrukcií a konkrétne sa zaoberá analýzou predpätia využitím nepriamych analyticko-experimentálnych metód, akou je aj metóda uvoľnenia napätí (saw-cut method).
Metóda bola testovaná na sérii meraní na vopred predpätých železničných podvaloch. Experimentálne výsledky sa porovnali s teoretickým výpočtom a následne sa platnosť výsledkov objektivizovala využitím konceptu podmienenej pravdepodobnosti – Bayesovho modelu.
Vo viacerých európskych krajinách sa značná časť infraštruktúry vybudovala v povojnovom období. Skúsenosti s havarijnými stavmi niekoľkých mostov z nedávnej minulosti ukazujú, že viaceré mosty, hlavne predpäté, sa blížia k hranici svojej životnosti už po približne 60 rokoch prevádzky.

Celkový stav existujúcich mostov odráža nielen úroveň rozvoja spoločnosti, v ktorej boli postavené, ale aj kultúrnu a ekonomickú silu súčasnej generácie, keďže odzrkadľuje starostlivosť o tieto zdedené inžinierske stavby. Pri týchto mostoch má predpätie rozhodujúci vplyv na ich celkovú statickú funkčnosť a spoľahlivosť, ktorá, ako sa ukazuje, v čase významne klesá.
Nie je to však len dôsledkom reologických vplyvov betónu, ale aj už od počiatku nevhodným stavom ochrany kotvenia, ako aj predpínacích jednotiek, ktoré následne korodujú, v kombinácii so značným preťažovaním mostov a s ich nedostatočnou údržbou [1].
V súčasnosti je k dispozícii niekoľko technicky akceptovateľných metód na stanovenie aktuálnej úrovne predpätia [1, 2]. Tieto metódy možno rozdeliť do dvoch hlavných skupín, na priame a nepriame metódy/techniky. Priame metódy vedú k stanoveniu predpínacej sily priamo z merania pomerných pretvorení alebo napätosti predpínacej jednotky.
Aplikácia týchto metód v existujúcich konštrukciách je však veľmi obmedzená presnosťou a technickými možnosťami merania. Preto sa ako najvhodnejšia alternatíva javí aplikácia semideštruktívnych nepriamych metód [2]. Nepriame metódy zahŕňajú napríklad metódy založené na systéme uvoľnenia napätia v betónovom prvku, napr. metóda saw-cut alebo tzv. metóda odozvy (structural response method) – systém znovuotvorenia trhliny [2].
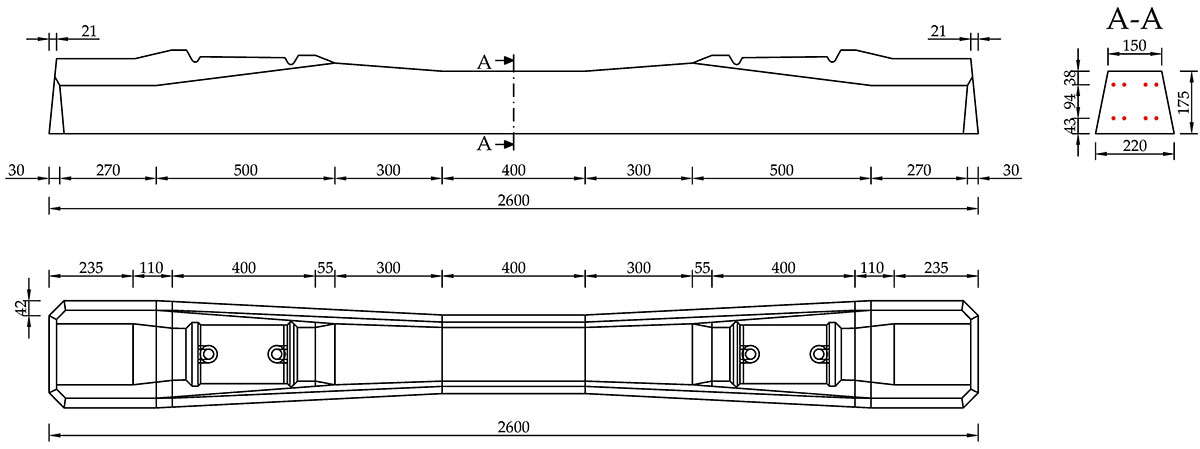
Tento príspevok je zameraný na testovanie spoľahlivosti saw-cut metódy v laboratórnych podmienkach na vopred predpätých prvkoch, aby sa v maximálnej možnej miere eliminovali neistoty merania vyplývajúce z aplikácie metódy in situ. Z toho dôvodu sa zvolila séria 3 ks predpätých betónových podvalov typu B70 W-49 G, ktorá bola skúšaná približne po roku od ich výroby (obr. 1).
Opis experimentálnych meraní
Ako už naznačuje názov metódy, iniciácia uvoľnenia normálových napätí sa realizovala vytvorením priečnych rezov cez podval na zvolených miestach na priamej ploche v strede podvalov tak, aby na každom podvale vznikli dva izolované betónové bloky, na ktorých sa sledovala zmena pomerných pretvorení pomocou nalepených odporových tenzometrov typu HBM LY41-50/120.
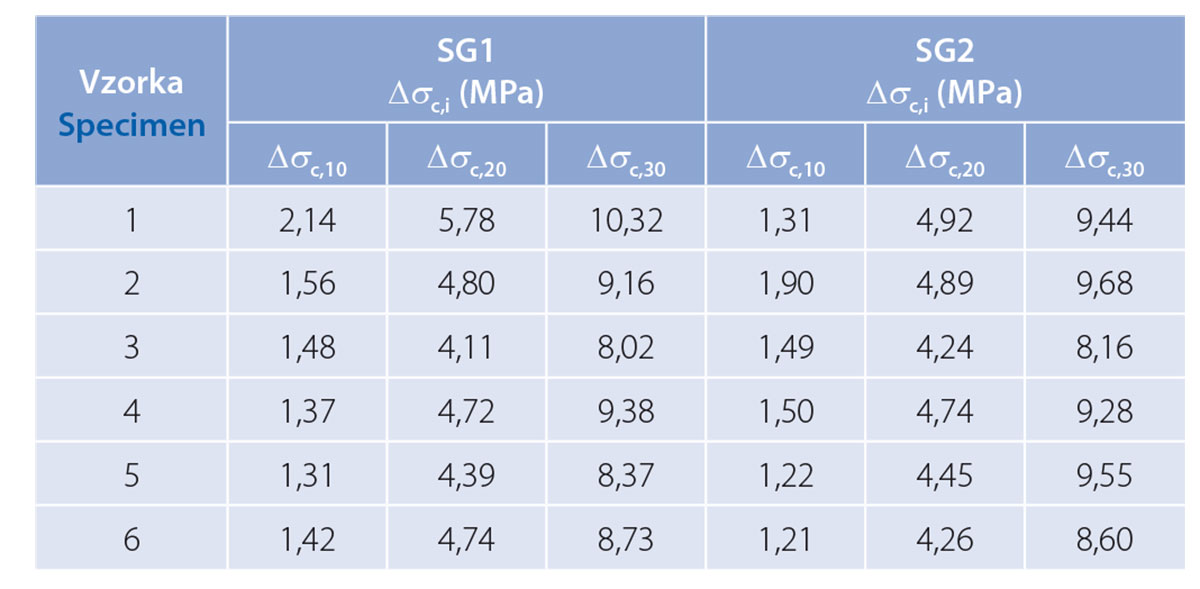
Vo všeobecnosti možno v prípade predpätého prvku bez trhlín odvodiť z uvoľnených hodnôt normálového napätia (Dsc,i) veľkosť predpínacej sily v danom čase Pm,t = Presidual podľa vzťahu.
Dva hlavné faktory, ktoré ovplyvňujú veľkosť uvoľneného normálového napätia, sú hĺbka a osová vzdialenosť vykonávaných rezov. V našom prípade sa rezy aplikovali postupne až do hĺbky 30 mm. Princíp metódy saw-cut je znázornený na obr. 2.

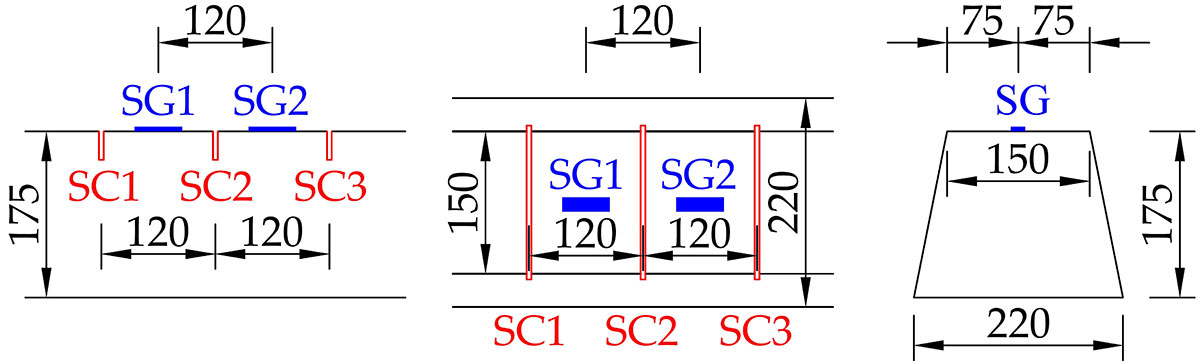
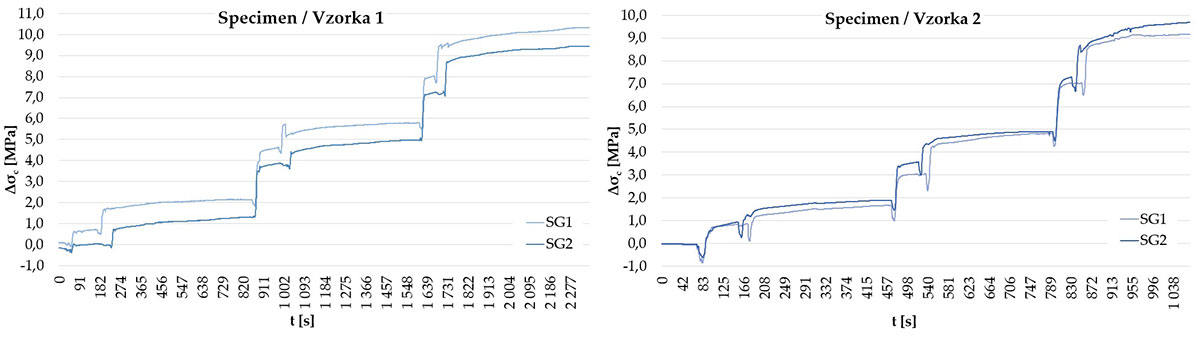
Takto sa v našom prípade získal súbor 6 meraní, ktorý sa ďalej štatisticky spracovával a vyhodnocoval v kombinácii s teoreticky stanovenými predpokladanými hodnotami na princípe podmienenej pravdepodobnosti, čo predstavuje v bayesovskom koncepte tzv. doplnkovú hypotézu (likelihood). Príklad postupného vývoja zmeny pomerných pretvorení na hornej ploche betónu podvalu č. 1 v dvoch blokoch dokumentuje obr. 3.
Aplikácia podmienenej pravdepodobnosti
Analytické alebo numerické výpočty predpokladanej úrovne predpätia v existujúcej konštrukcii sa považujú vo všeobecnosti za štandardný prístup (Pcalc). Vstupné údaje aplikované do procesu učenia predpínacej sily sa získavajú ako výsledky diagnostiky, a teda majú prirodzene silne stochastický charakter – apriórna hypotéza, resp. tzv. priórna pravdepodobnosť.
Najmä materiálové parametre betónu, predpínacia výstuž a, samozrejme, v značnej miere reologické procesy v podobe dotvarovania a zmrašťovania betónu vplývajú na predpínaciu silu v čase. Neistoty v získavaní dát (miesto merania, početnosť a pod.) možno do veľkej miery eliminovať štatistickým spracovaním získaného súboru.
Presnosť však závisí od rozsiahlosti súboru dát. Aby bolo možné relevantne spracovať výsledný náhodný jav (hypotéza) predstavujúci v našom prípade predpínaciu silu v čase, je potrebné zvyšné hodnoty dosimulovať, pričom je vhodné využiť niektorú zo simulačných techník, napr. metódu Monte Carlo.
Týmto spôsobom sa generovali náhodné vektory všetkých vstupných premenných veličín (1 000 hodnôt), ktoré definovali vstupné hypotézy pre podmienenú bayesovskú pravdepodobnosť [4].
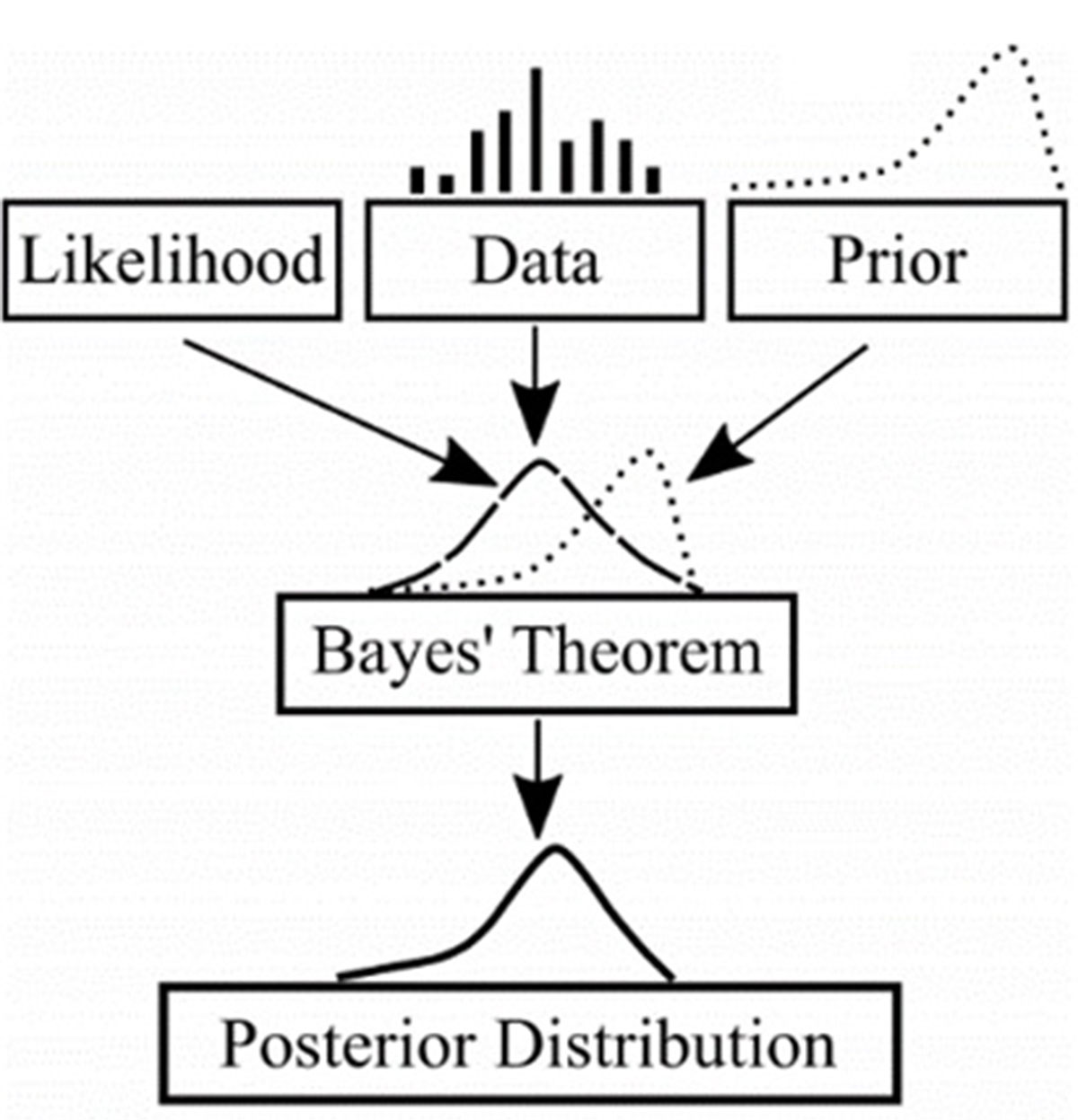
Bayesov princíp v zmysle podmienenej pravdepodobnosti dokážeme využiť pri stanovení tzv. objektívnej pravdy v systéme dvoch alebo viacerých závislých javov, resp. hypotéz [4]. Základný princíp je stručne opísaný na príklade dvoch javov (hypotéz) A a B.
Podmienená pravdepodobnosť P(A|B) (nazývaná aj posteriórna pravdepodobnosť) javu A vzniká vtedy, ak je jav B pravdivý a nastal s nenulovou pravdepodobnosťou P(B). Graficky je možné proces stanovenia výsledného rozdelenia posteriórnej pravdepodobnosti spojitej náhodnej premennej (predpínacia sila Ppost) interpretovať podľa obr. 4.
V našom prípade mali náhodné veličiny normálne rozdelenie, čo bolo verifikované testom spoľahlivosti Q-Q-plot pre doplnkovú hypotézu (obr. 5). Medzinárodná organizácia Joint Committee on Structural Safety (JCSS) v nosnom dokumente [4] odporúča využiť riešenie rovnice vyplývajúcej z princípu (2) v upravenom tvare a funkciu hustoty priórnej pravdepodobnosti vyjadriť v inžiniersky prijateľnej forme pomocou rozdelenia s m a s vo forme
Toto rozdelenie pravdepodobnosti spojitej náhodnej veličiny je potom transformované podľa [3, 4] do posteriórnej pravdepodobnosti f’’(m, s) za pomoci konjugácie doplnkovej hypotézy.
Vyhodnotenie Bayesovho konceptu
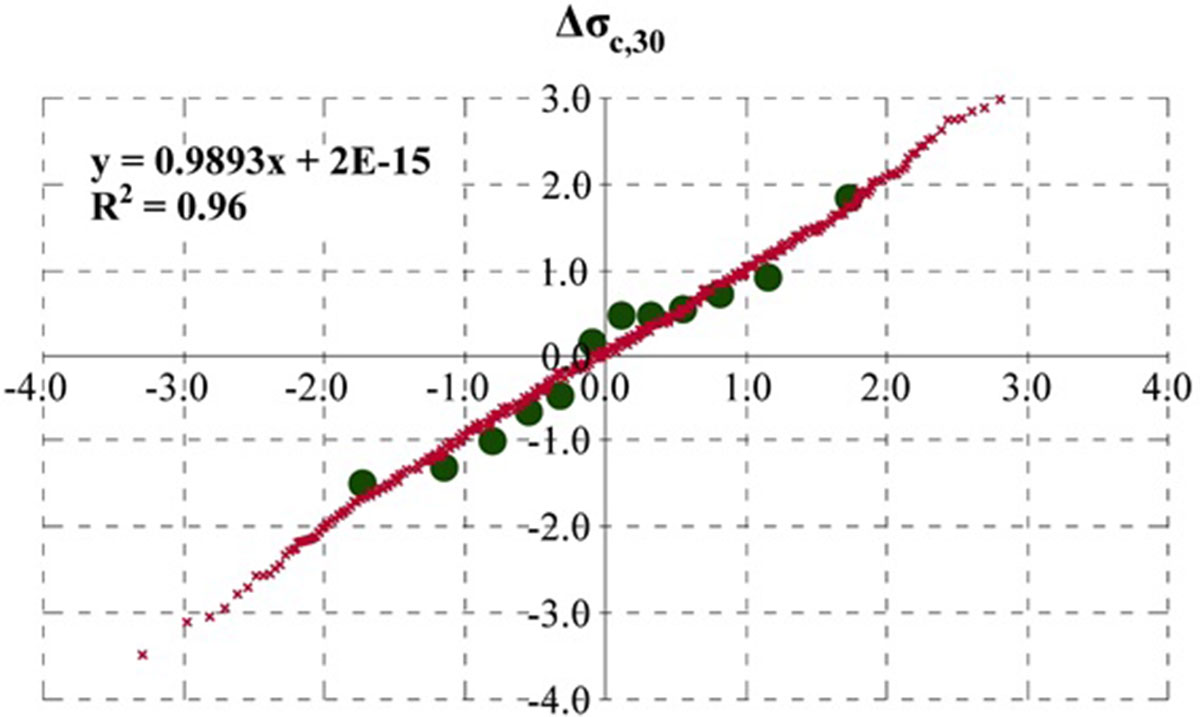
Analýza sa realizovala na viacerých úrovniach rezov, vzhľadom na rozsah článku však uvádzame len stanovenie rozdelenia náhodného vektora aktuálnej predpínacej sily pre rezy s uvoľneným napätím na úrovni hĺbky 30 mm, Presidual = P30 = {P (30 mm)}. Tieto údaje sú ďalej na obr. 6 dokumentované funkciami rozdelenia pravdepodobnosti vo forme PDF (distribučná funkcia hustoty pravdepodobnosti) a CDF (kumulatívna distribučná funkcia).
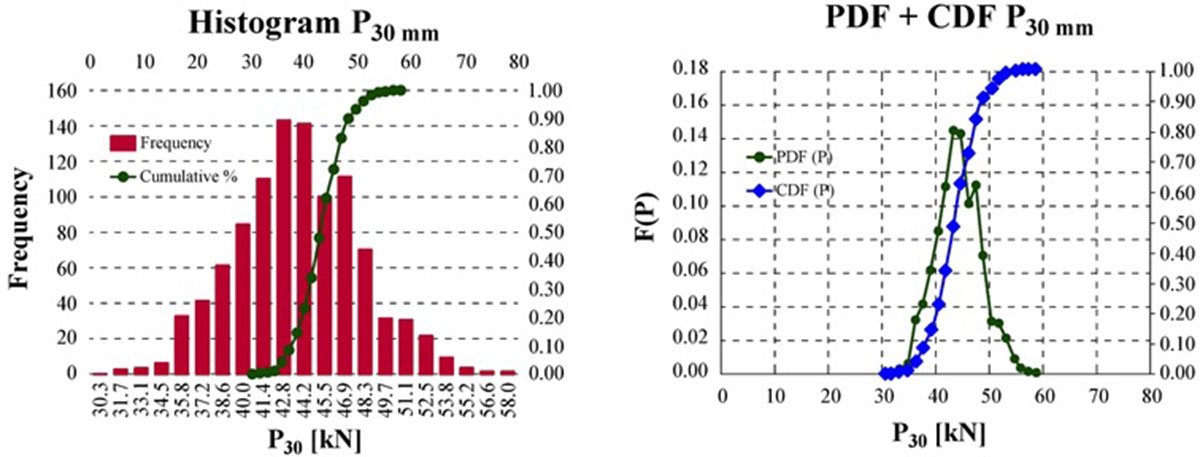
V tab. 1 sú prehľadne uvedené všetky hodnoty uvoľnených napätí v jednotlivých rezoch. Prediktívny súbor údajov analyticky vypočítanej predpínacej sily {Pcalc} bol vyššie prezentovaný ako priórna hypotéza s funkciou rozdelenia náhodnej premennej f'(m, s) podľa rovnice (3).
Náhodný vektor Presidual = {P (30 mm)} odvodený zo zmeny normálového napätia a zodpovedajúci zvolenej hĺbke rezu bol aplikovaný v bayesovskom modeli ako doplnková podmieňujúca hypotéza. Takáto funkcia založená na súbore nameraných údajov z rezovej metódy špecifikuje a aktualizuje výpočtovú predikciu.
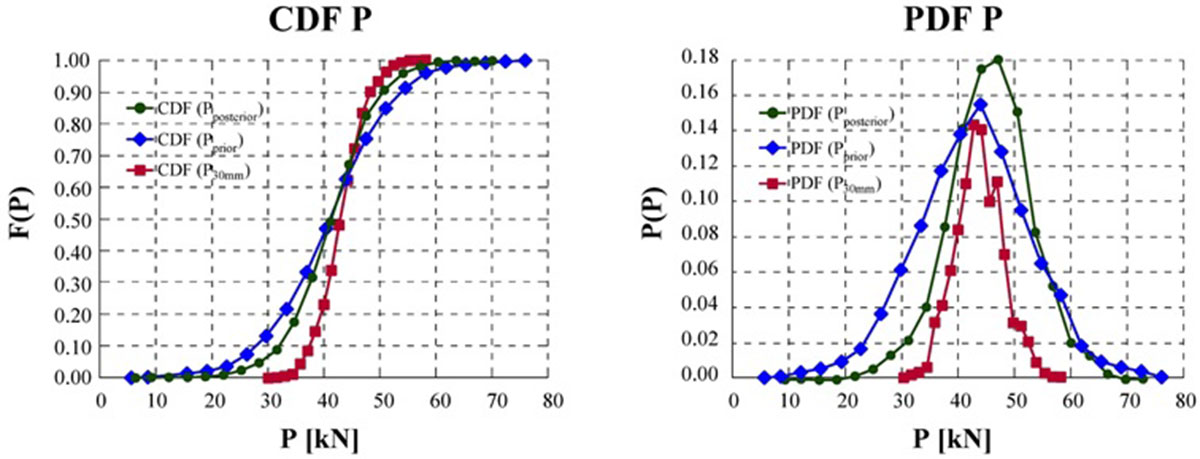
Výsledná distribučná funkcia predpínacej sily {Ppost = P} je uvedená ako posteriórna pravdepodobnostná funkcia s rozdelením f“(m, s). Konjugáciu oboch funkcií možno vykonať pomocou simulačných techník, napríklad simulácie MCM, a výsledok možno graficky interpretovať vo funkciách rozdelenia pravdepodobnosti PDF a CDF – pre predpínaciu silu {Ppost} (obr. 7).
Záver
Rozhodujúcim faktorom pri posudzovaní existujúcich predpätých betónových konštrukcií je stanovenie hodnoty predpínacej sily v danom čase. Objektívne určenie tejto hodnoty predstavuje vo všeobecnosti veľmi náročnú úlohu a vyžaduje si často len experimentálno-teoretický prístup.
V prezentovanej štúdii boli ako testovacie telesá zvolené 3 ks vopred predpätých podvalov s jasne definovanou hladinou predpätia v prakticky dokonalom technickom stave rok po výrobe, uložené v stabilných podmienkach skladu. Úroveň predpínacej sily v čase bola stanovená štandardným výpočtom podľa EC2 s uvážením príslušných strát predpätia, pričom jej stredná hodnota bola Pm,t = 40,96 kN.
Simuláciou MC sa získal vektor náhodnej premennej s normálnou distribúciou {Pcalc}. V tomto článku je uvedená doplnková hypotéza na základe experimentálnej rezovej metódy pre 30 mm hlboký rez {P (30 mm)}. Bayesov koncept podmienenej pravdepodobnosti umožnil následne získať „najpravdepodobnejšiu“ hodnotu sledovanej náhodnej veličiny {Ppost}.
V našom prípade je stredná hodnota posteriórneho rozdelenia Ppost = 41,34 kN. V tomto prípade vykazujú obe funkcie takmer zhodu (obr. 7). Ak by však tvar, distribúcia a posun na osi X pri prediktívnej funkcii a funkcii doplnkovej hypotézy boli vzdialené, funkcia rozdelenia posteriórnej pravdepodobnosti by bola významne rozdielna.
Predpätie je kľúčovou informáciou pri určovaní únosnosti existujúcich predpätých betónových konštrukcií a aplikácia Bayesovho modelu štatistického hodnotenia dokáže nepochybne veľmi objektivizovať tak silne stochastický jav, akým je stanovenie hodnoty aktuálnej úrovne predpätia v čase.
Príspevok vznikol s podporou projektov VEGA 1/0306/21 a 1/0048/22 a projektu KEGA 020ŽU-4/2021.
Literatúra
1. Moravčík, M. – Bujňáková, P. – Bahleda, F.: Failure and damage of a first-generation precast prestressed bridge in Slovakia. Structural Concrete 2020, 21, 2353 – 2362, doi:10.1002/suco.201900526.
2. Bagge, N. – Nilimaa, J. – Elfgren, L.: In-situ Methods to Determine Residual Prestress Forces in Concrete Bridges. Engineering Structures; 2017.
3. Botte, W. – Vereecken, E. – Taerwe, L. – Caspeele, R.: Assessment of posttensioned concrete beams from the 1940s: Large-scale load testing, numerical analysis and Bayesian assessment of prestressing losses. Structural Concrete 2021, 22(5).
4. JCSS: Probabilistic Model Code, Retrieved from: https://www.jcss-lc.org/jcss-probabilistic-model-code. 2001.













































