Korelácie statických a dynamických charakteristík kontroly kvality zhutnenia nestmelených konštrukcií vozoviek
Od zemnej konštrukcie sa vyžaduje jej dlhodobá funkčnosť vzhľadom na to, že je integrálnou súčasťou rozsiahlejšej, finančne náročnejšej dopravnej stavby (diaľnice, cesty, železničné dráhy, vzletovo-pristávacie a pojazdné dráhy, spevnené a odstavné plochy).
 |
Poznáte výhody Klubu ASB? Stačí bezplatná registrácia a získate sektorové analýzy slovenského stavebníctva s rebríčkami firiem ⟶ |
Situáciu v tejto oblasti komplikuje skutočnosť, že okamžité ekonomické a politické záujmy hlavných účastníkov výstavby, predovšetkým investora, bývajú, žiaľ, v praxi nezriedka nadraďované dlhodobejším, trvalo udržateľným cieľom. Ide napríklad o snahu urýchliť čas výstavby. resp. neprekročiť za žiadnu cenu predpokladané finančné náklady.
Pri hodnotení kvality zemných konštrukcií dopravných stavieb je, podobne ako pri ostatných stavebných súčastiach dopravnej infraštruktúry, nevyhnutné uplatniť systémový prístup zohľadňujúci oprávnené požiadavky užívateľov, obyvateľov okolia pozemných komunikácií (PK), ako aj ekonomickú úroveň spoločnosti [1].
V prácach [2 až 4] sme prezentovali syntézu existujúcich domácich aj zahraničných poznatkov, normových postupov a objektivizovaných výsledkov výskumu autorov, ktorá vytvorila teoretický základ pre systémový prístup k hodnoteniu kvality zemných konštrukcií dopravných stavieb v podmienkach SR.
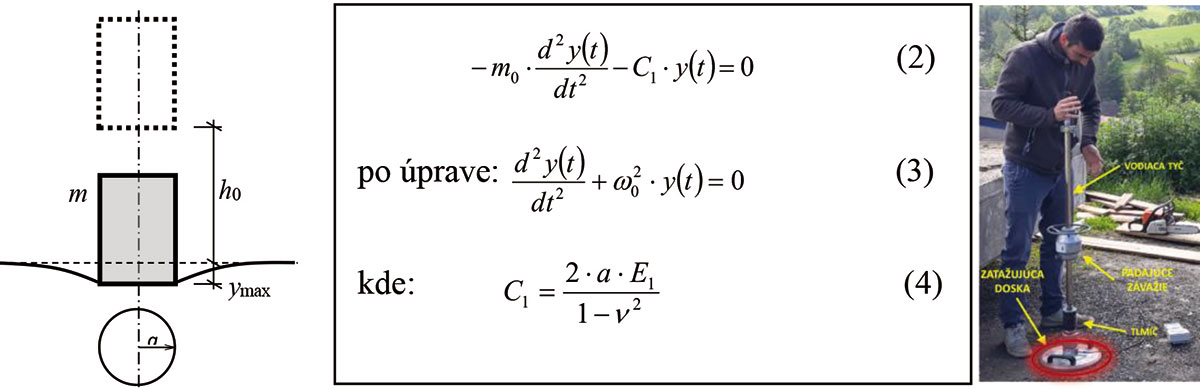
VYNEKOVO | Zdroj: autor
Vo vedeckom príspevku z roku 2011 [5] a následne vo vedeckých monografiách [2] a [6] autori prezentovali teoreticky zdôvodnenú a pre prax veľmi dôležitú korelačnú závislosť modulu deformácie z druhého zaťažovacieho cyklu Edef, 2 meraného podľa STN 736190 [7] od dynamického modulu deformácie Evd, zisťovaného podľa postupu STN 73 6192 [8].
Prezentovaná korelačná závislosť bola určená na základe meraní autorov z obdobia rokov 1995 až 2010 na rôznych druhoch nestmelených konštrukčných vrstiev vozoviek a podložia PK. Predkladaný príspevok prezentuje verifikáciu predmetnej závislosti na základe výsledkov meraní autorov tohto článku z obdobia rokov 2000 až 2020.
Inžinierska teória nárazu
Podľa [5] patrí statická teória nárazu medzi približné teórie riešenia nárazu tuhého telesa na pružný polpriestor. Na účely potrieb inžinierskej praxe sa zavádzajú zjednodušujúce predpoklady, ktoré nemajú podstatný vplyv na výpočtové hodnoty charakteristík nárazu.
Medzi tlakovou silou P (MN) (kolmou na styčnú rovinu) a zatlačením y (m) platí vzťah:
Na obr. 1 je uvedený princíp riešenia nárazu tuhého telesa na pružný polpriestor a pohľad na zariadenie LDD 100 pri meraní dynamického modulu deformácie Evd na pokusnom poli pri výskume nestmelených konštrukcií vozoviek (PP VYNEKOVO) v Pekline.
Celý náraz predstavuje jednu polovicu kmitu a prebehne za polovicu periódy kmitania T0. Čas nárazu tr (s) sa tak rovná:
Maximálne zatlačenie ymax sa vypočíta ako:
Maximálna nárazová sila Pmax sa určí pomocou rovnice:
V rovniciach (2) až (9) vystupujú tieto premenné:
ω0 – uhlová frekvencia pohybu, pričom:
ω = 2π . v/L (rad/s), (8)
c0 – rýchlosť pri dopade tuhého telesa (m/s),
h0 – výška pádu tuhého telesa (m),
m0 – hmotnosť tuhého telesa (kg),
g – tiažové zrýchlenie (m/s2).
Rýchlosť pri dopade tuhého telesa na pružný polpriestor sa určí podľa rovnice (9) ako
Korelácie Edef, 2 od Ep, n a Evd zistené z výsledkov meraní v rokoch 1995 až 2010
V nemeckej, českej a slovenskej literatúre sa v období rokov 1990 až 2010 uvádzali korelačné závislosti medzi hodnotami dynamického modulu deformácie Evd meraného zariadením LDD 100 a hodnotami Edef, 2 vyhodnocovanými zo statickej zaťažovacej skúšky (SZS) prezentované predovšetkým v tvare:
Edef,2 = k SZS/LDD100 . E vd (10)
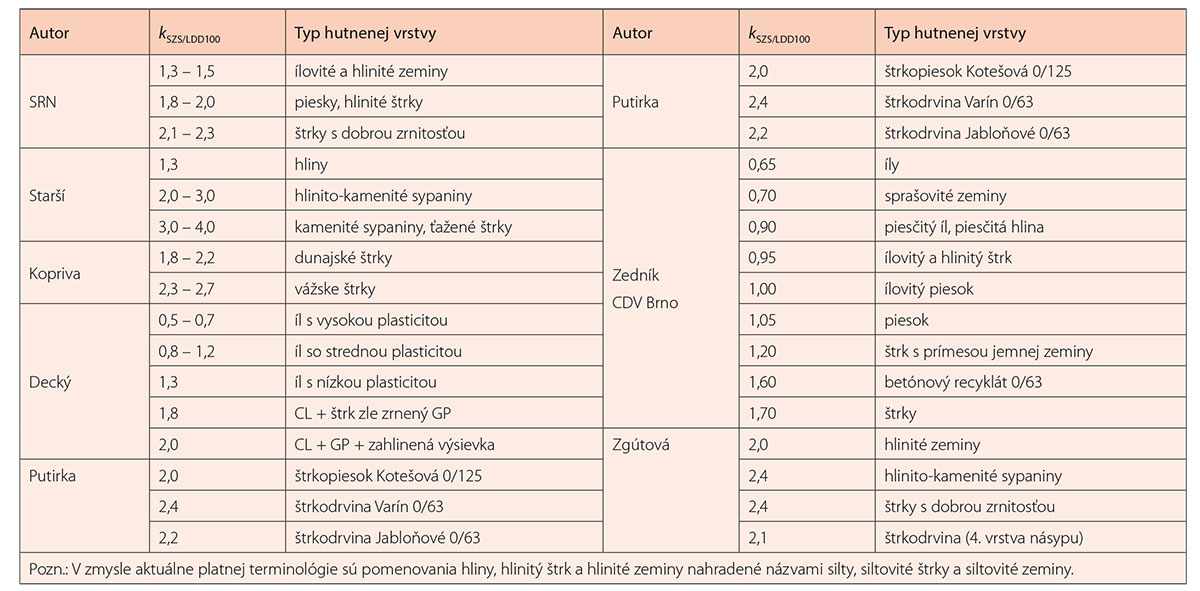
V tab. 1 je uvedený prehľad rozsahov hodnôt koeficientu kSZS/LDD100 (15) uvádzaných rôznymi autormi. Vo vedeckom príspevku z roku 2011 [5] autori prezentovali prvýkrát korelačné závislosti (KZ):
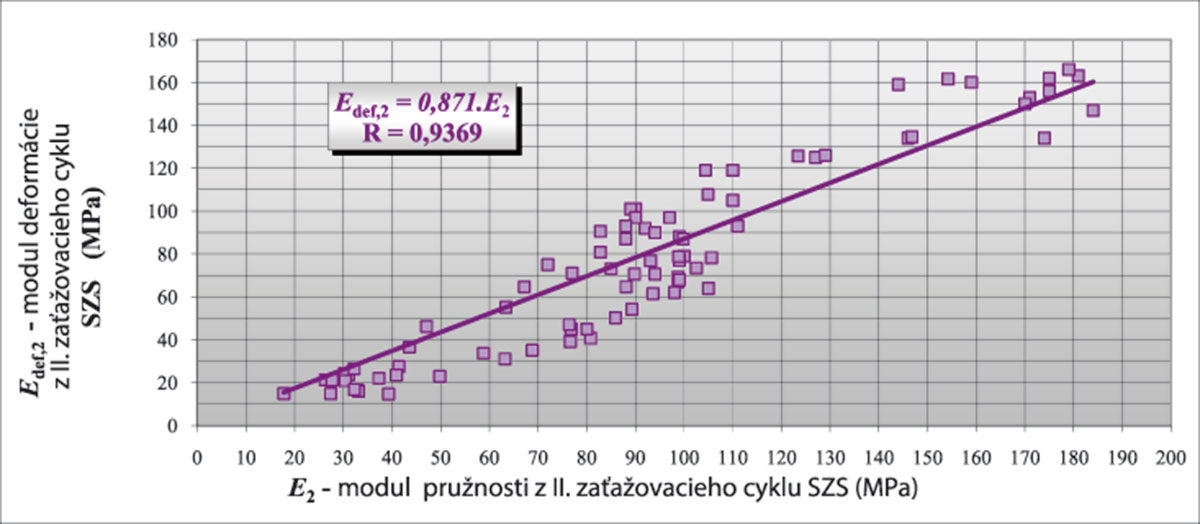
- modulu deformácie z druhého zaťažovacieho cyklu Edef, 2 od modulu pružnosti E2 (obr. 2) vyhodnotených z meraní statickej zaťažovacej skúšky (SZS) podľa STN 73 6190 [7] porovnateľných s angloamerickými postupmi [8],
- modulu deformácie Edef, 2 od dynamického modulu deformácie Evd (obr. 3) meraných podľa postupu STN 73 6192 zariadením LDD 100 [9].
V rámci výskumu autori zistili, že modul pružnosti týchto konštrukčných vrstiev PK je prakticky identický pri 1. aj 2. zaťažovacom cykle SZS a je ekvipolentný s návrhovou hodnotou modulu pružnosti určeného z výsledkov skúšky CBR [10].
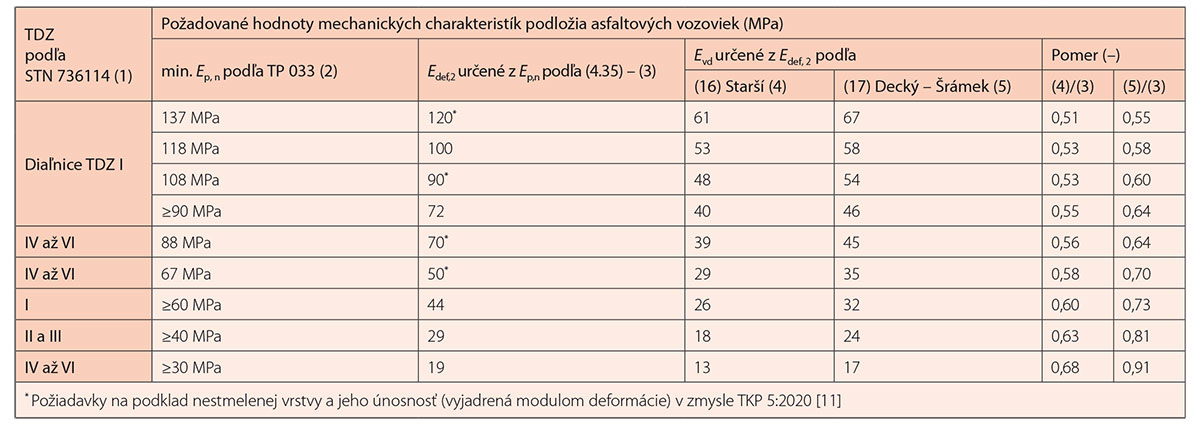
Z tab. 2 vyplýva, že pri navrhovaní asfaltových vozoviek PK v zmysle kodifikovaných ustanovení cestného zákona č. 135/1961 Zb. [12] a technických podmienok TP 033 [13] by sa malo počítať s modulmi pružnosti zodpovedajúcimi požadovaným hodnotám Edef, 2.
Hodnoty zvýraznené na obr. 3 modrou elipsou predstavujú závislosti z nedostatočne zhutnenej tunelovej rúbaniny použitej ako ochranná vrstva vozovky v tuneli, pri ktorých sa pomery Edef, 2 /Edef, 1 pohybovali v rozsahu od 2,9 do 4,5.
Analýzou dosiahnutých výsledkov a s využitím rovníc (1) až (9) sa zistilo, že koeficient kSZS/LDD100 nadobúda hodnotu 1,0 pri hodnote modulu deformácie Edef, 2 = 25 MPa.
Z uvedeného je zrejmé, že pri tejto hodnote budú rovnaké deformačné charakteristiky zistené SZS a zariadením LDD 100 pri výške pádu 0,75 m, čo je konštantná hodnota používaná v technickej praxi. Na základe prezentovaných skutočností možno konštatovať, že zariadenie LDD 100 generuje kontaktný tlak 0,1 MPa pod doskou práve pri hodnote E = 25 MPa.
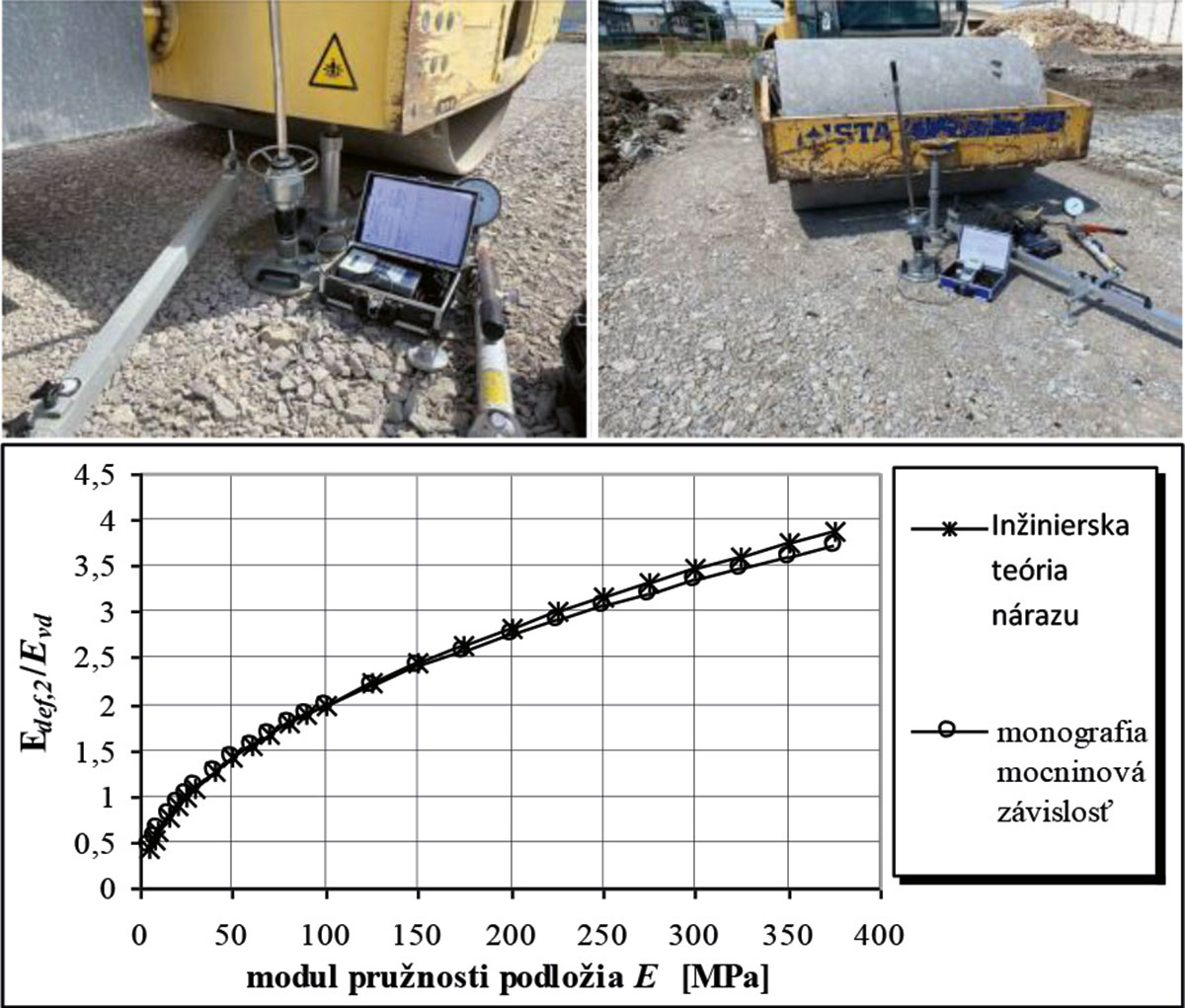
Na obr. 4 je prezentovaná komparácia hodnôt kSZS/LDD100 = Edef, 2/Evd, zistených v rámci výskumných aktivít pracovníkov SvF UNIZA označená ako monografia – mocninová závislosť s teoretickými hodnotami zistenými podľa inžinierskej teórie nárazu. Hodnoty k SZS/LDD100 boli v prípade inžinierskej teórie nárazu určené podľa vzťahu:
- kde Pmax, Ei je max. amplitúda nárazovej sily pri hodnote modulu pružnosti podložia Ei (kN),
- Pmax, E = 25 MPa – max. amplitúda nárazovej sily pri module pružnosti podložia E =25 MPa (kN).
Korelácie Edef, 2 od Evd, LDD100 zistené z výsledkov meraní v rokoch 2000 až 2020
Na obr. 5 je prezentovaná korelačná závislosť hodnoty Edef, 2 určenej SZS podľa STN 73 6190 od modulu deformácie meraného zariadením LDD 100 objektivizovaná z dlhoročných výsledkov meraní pracovníkov SvF UNIZA (2000 až 2020) a významných odborníkov z praxe (RNDr.
Boris Starší, modrá krivka na obr. 5). Pri určení korelačnej závislosti Decký – Šrámek sa už nepočítalo s hodnotami na obr. 3 nachádzajúcimi sa v modrej elipse. Prepočet hodnôt Edef, 2 na hodnoty Evd uvedený v tab. 3 sa uskutočnil úpravou rovníc uvedených na obr. 5 na tvar (16) a (17).
Na základe dlhodobého výskumu, ktorý prebiehal na pracovisku autorov v spolupráci s významnými odborníkmi z praxe, možno vo vzťahu k navrhovaniu a kontrole kvality zemných konštrukcií v podmienkach SR vysloviť tieto odporúčania:
- je potrebné zjednotiť a podrobnejšie špecifikovať kritériá požadovanej únosnosti podložia dopravných stavieb, používané v štádiu navrhovania a kontroly výstavby stavieb,
- na kontrolu únosnosti a miery zhutnenia zemných konštrukcií by sa mala prednostne používať statická zaťažovacia skúška (SZS),
- v prípade nemožnosti použiť SZS vo vzťahu k zariadeniu LDD 100 používať v prípade kvázipružných polpriestorov (neplatí pri viacvrstvových systémoch s výrazne rozdielnymi modulmi pružnosti) orientačné prepočítavacie koeficienty podľa rovnice (18) (obr. 5).
V tomto čase intenzívnej prípravy a výstavby dopravnej infraštruktúry SR, rekonštrukcií regionálnych a miestnych komunikácií spolufinancovaných z fondov EÚ by aplikácia uvedených poznatkov do praxe mohla pomôcť optimalizácii vynakladania finančných prostriedkov v predmetnej oblasti.
Jednotné kritériá na meranie SZS a ich kompatibilita s výsledkami meraní zariadenia LDD 100 umožnia „kvalitárom“ pôsobiacim v oblasti dopravných stavieb jednoznačne určovať závery v mieste merania, čím sa dosiahne zjednodušené riadenie inžinierskej stavby.
Prezentované odporúčania v navrhovaní PK možno aplikovať z aspektu ustanovenia cestného zákona [12] uvádzajúceho v §2, ods. 4, že navrhovanie pozemných komunikácií sa vykonáva podľa platných slovenských technických noriem, technických predpisov, objektívne zistených výsledkov výskumu a vývoja pre cestnú infraštruktúru alebo obdobných technických špecifikácií.
TEXT: prof. Dr. Ing. Martin Decký,
RNDr. Boris Starší, doc. Ing. Juraj Šrámek, PhD., prof. Ing. Marián Drusa, PhD.
FOTO A OBRÁZKY: autori
Martin Decký, Marián Drusa a Juraj Šrámek pôsobia na SvF UNIZA v Žiline, Marián Drusa je dekanom tejto fakulty. Boris Starší pôsobí v spoločnosti KVALITEST.
- DECKÝ, M., PITOŇÁK, M., JUHÁS, M. a kol.: Holistické prístupy k trvalo udržateľnej výstavbe a správe pozemných komunikácií. In Inžinierske stavby, ročník 68, vyšlo 6.7.2020 (č. 03/2020), s. 20 – 22.
- DRUSA, M., DECKÝ, M., MARSCHALKO, M. a kol.: Navrhovanie a kontrola zemných konštrukcií dopravných stavieb. Vedecká monografia, EDIS – vydavateľstvo ŽU 2013, s. 522.
- ŠRÁMEK, J.: Životný cyklus asfaltových vozoviek. Habilitačná práca, SvF UNIZA 2019, s. 99.
- DECKÝ, M., ZUZULOVÁ, A., DREVENÝ, I. a kol.: Cementobetónové vozovky a spevnenia dopravných plôch. Navrhovanie, posudzovanie, materiály, poruchy, rehabilitácie, BIM. Vysokoškolská učebnica, 2. prepracované vydanie, Žilinská univerzita v Žiline, EDIS – vydavateľské centrum ŽU 2020, s. 401.
- DECKÝ, M., ZGÚTOVÁ, K., PITOŇÁK, M.: Kontrola kvality zhutnenia zemných konštrukcií dopravných stavieb. In Silniční obzor, 4/2011, s. 101 – 108.
- DECKÝ, M., DRUSA, M., PEPUCHA, L., ZGUTOVA, K.: Earth Structures of Transport Constructions. Scientific monograph, London: Pearson Education Limited, Edidburg Gate, Harlow 2013. Editor: prof. Dr. Ing. Martin Decký, s. 180.
- STN 73 6190 Statická zaťažovacia skúška stavebných konštrukcií doskou, 2019.
- MALLICK, R., B., EL-KORCHI, T.: Pavement Engineering. Principles and Practise. Third edition, CRC Press 2018 by Taylor&Francis Group, p. 747.
- STN 73 6192 Rázová zaťažovacia skúška vozoviek a podložia, 2011.
- STN 72 1016 Laboratórne stanovenie pomeru únosnosti zemín (CBR), 1992.
- TKP 5 Podkladové vrstvy z nestmelených a hydraulicky stmelených zmesí, MDV SR 2020.
- Zákon č. 135/1961 Zb. Zákon o pozemných komunikáciách (cestný zákon) v znení neskorších predpisov.
- TP 033 Navrhovanie netuhých a polotuhých vozoviek, MDPT SR 2009.





![Obr. 2b Obr. 2 Mocninová a lineárna závislosť modulu deformácie z druhého zaťažovacieho cyklu Edef, 2 od hodnoty modulu pružnosti podložia a nestmelených vrstiev vozoviek PK [5]](https://www.asb.sk/wp-content/uploads/2024/06/Obr.-2b.jpg)
![obr 3 Obr. 3 Mocninová a lineárna závislosť modulu deformácie z druhého zaťažovacieho cyklu Edef, 2 od dynamického (rázového) modulu deformácie meraného zariadením LDD 100 [5]](https://www.asb.sk/wp-content/uploads/2024/06/obr-3.jpg)
![01 56 IS321 38 Tab. 2 Prepočítané požadované hodnoty podkladu nestmelenej vrstvy vozoviek podľa TKP 5:2020 [11]](https://www.asb.sk/wp-content/uploads/2024/06/01_56_IS321-38.jpg)
![Obr. 5 Obr. 5 Mocninová a lineárna závislosť modulu deformácie z druhého zaťažovacieho cyklu Edef, 2 od návrhovej hodnoty modulu pružnosti podľa [5]](https://www.asb.sk/wp-content/uploads/2024/06/Obr.-5.jpg)